When you are operating on geographical data you can use latitude and longitude to specify a location somewhere on earth. To look up some associated information like we do in GraphHopper for the next street or if you want to do neighborhood searches you could create R-trees, quad-trees or similar spatial data structures to make them efficient. Some people are using Geohashes instead because then the neighborhood searches are relative easy to implement with simple database queries.
In some cases you’ll find binary representations of Geohashes – I named them spatial keys – in the literature I found a similar representation named locational code (Gargantini 1982) or QuadTiles at OpenStreetMap. A spatial key works like a Geohash but for the implementation a binary representation instead of one with characters is chosen:
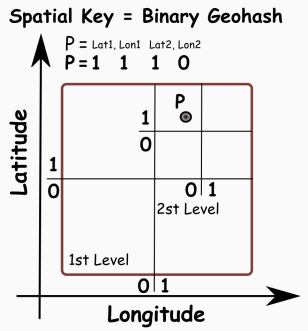
At the first level (e.g. assume world boundaries) for the latitude we have to decide whether the point is at the northern (1) or southern (0) hemisphere. Then for the longitude we need to know wether it is in the west (0) or in the east (1) of the prime meridian resulting in 11 for the image below. Then for the next level we “step into” smaller boundaries (lat=0..90°,lon=0..+180°) and we do the same categorization resulting in a spatial key of 4 bits: 11 10
The encoding works in Java as follows:
long hash = 0;
double minLat = minLatI;
double maxLat = maxLatI;
double minLon = minLonI;
double maxLon = maxLonI;
int i = 0;
while (true) {
if (minLat midLat) {
hash |= 1;
minLat = midLat;
} else
maxLat = midLat;
}
hash <<= 1;
if (minLon midLon) {
hash |= 1;
minLon = midLon;
} else
maxLon = midLon;
}
i++;
if (i < iterations)
hash <<= 1;
else
break;
}
return hash;
When we have calculated 25 levels (50 bits) we are in the same range of float precision. The float precision is approx. 1m=40000km/2^25 assuming that for a lat,lon-float representation we use 3 digits before the comma and 5 digits after. Then a difference of 0.00001 (lat2-lat1) means 1m which can be easily calculated using the Haversine formula. So, with spatial keys we can either safe around 14 bits per point or we are a bit more precise for the same memory usage than using 2 floats.
I choose the definition Lat, Lon as it is more common for a spatial point, although it is against the mathematic point x,y.
Now that we have defined the spatial key we see that it has the same properties as a Geohash – e.g. reducing the length (“removing some bits on the right”) results in a broader matching region.
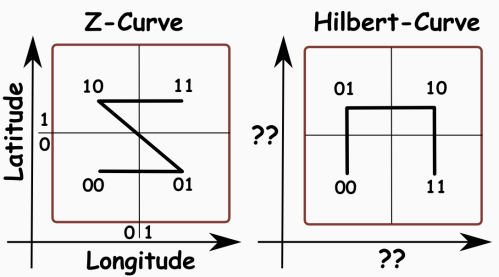
Additionally the order of the quadrants could be chosen differently – instead of the Z-curve (also known as Morton Code) you could use the Hilbert Curve:
But as you can see, this would make the implementation a bit more complicated and e.g. the orientation of the “U” order depends on previous levels – but the neighborhood searches would be more efficient – this is also explained a bit in the paper Speeding Up Construction of Quadtrees for Spatial Indexing p.8.
I decided to avoid that optimization. Let me know if you have some working code of SpatialKeyAlgo for it 🙂 ! It should be noted that there are other space filling curves like the ones from Peano or Sierpinsky.
One problem
while implementing this was to get the same point out of decode(encode(point)) again. The encoding/decoding schema needs to be “nearly bijective” – i.e. it should avoid rounding problems as good as possible. To illustrate where I got a problem assume that the point P (e.g. see the image above) is encoded to 1110 – so we already lost precision, when our point is now at the bottom left of the quadrant 1110. Now if we decode it back we loose again some precision due to normal double rounding errors. If we would encode that point again it could end up as 1001 – the point moved one quadrant to the right and one to the bottom! To avoid that, you need to define position of the point at the center of the quadrant while decoding. I implemented this simply by adding half of the quadrant width to the latitude and longitude. This makes the encoding/decoding stable even if there are minor rounding issues while decoding.
A nice property of the spatial key
is that one bounding box e.g. for the starting bits at level 6:
110011
goes from the bottom left point
110011 0000..
to the top-right point
110011 1111..
making it easy to request e.g. the surrounding bounding boxes of a point for every level.
Conclusion
As we have seen the spatial key is just a different representation of a Geohash with the same properties but uses a lot less memory. The next time you index Geohashes in your DB use a long value instead of a lengthy string.
In the next post you will learn how we can implement a memory efficient spatial data structure with the help of spatial keys. If you want to look at a normal quadtree implemented with spatial keys you can take a look right now at my GraphHopper project. With this quadtree neighborhood searches are approx. twice times slower than one with values for latitude and longitude due to the necessary encoding/decoding. Have a look into the performance comparison project.
Pingback: Tricks to Speed up Neighbor Searches of Quadtrees. #geo #spatial #java « Find Time for the Karussell
Pingback: Failed Experiment: Memory Efficient Spatial Hashtable « Find Time for the Karussell
Pingback: Running Shortest-Path Algorithms on the German Road Network within a 1.5GB JVM « Find Time for the Karussell